Funzione potenza con esponente naturale e intero. Funzione potenza, sue proprietà e grafico Materiale dimostrativo Lezione frontale Concetto di funzione

Funzione dove X– quantità variabile, UN– viene chiamato un determinato numero Funzione di potenza .

Se quindi è una funzione lineare, il suo grafico è una retta (vedi paragrafo 4.3, Fig. 4.7).

Se quindi è una funzione quadratica, il suo grafico è una parabola (vedi paragrafo 4.3, Fig. 4.8).

Se allora il suo grafico è una parabola cubica (vedi paragrafo 4.3, Fig. 4.9).

Funzione di potenza

Questa è la funzione inversa di

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione è strana.

4. Frequenza della funzione: non periodico.

5. Zeri di funzione: X= 0 – l'unico zero.

6. La funzione non ha un valore massimo o minimo.

8. Grafico di una funzione Simmetrico al grafico di una parabola cubica rispetto ad una retta Y=X ed è mostrato in Fig. 5.1.

Funzione di potenza

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione è pari.

4. Frequenza della funzione: non periodico.

5. Zeri di funzione: zero singolo X = 0.

6. I valori più grandi e più piccoli della funzione: assume il valore più piccolo per X= 0, è uguale a 0.

7. Intervalli di aumento e diminuzione: la funzione è decrescente nell'intervallo e crescente nell'intervallo

8. Grafico di una funzione(per ciascuno N Î N) è “simile” al grafico di una parabola quadratica (i grafici delle funzioni sono mostrati in Fig. 5.2).

Funzione di potenza

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione è strana.

4. Frequenza della funzione: non periodico.

5. Zeri di funzione: X= 0 – l'unico zero.

6. Valori massimi e minimi:

7. Intervalli di aumento e diminuzione: la funzione è crescente nell'intero dominio di definizione.

8. Grafico di una funzione(per ciascuno ) è “simile” al grafico di una parabola cubica (i grafici delle funzioni sono mostrati in Fig. 5.3).

Funzione di potenza

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione è strana.

4. Frequenza della funzione: non periodico.

5. Zeri di funzione: non ha zeri.

6. I valori più grandi e più piccoli della funzione: la funzione non ha i valori più grande e più piccolo per nessuno

7. Intervalli di aumento e diminuzione: la funzione decresce nel suo dominio di definizione.

8. Asintoti:(asse UO) – asintoto verticale;

(asse OH) – asintoto orizzontale.

9. Grafico di una funzione(per chiunque N) è “simile” al grafico di un'iperbole (i grafici delle funzioni sono mostrati in Fig. 5.4).

Funzione di potenza

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione è pari.

4. Frequenza della funzione: non periodico.

5. I valori più grandi e più piccoli della funzione: la funzione non ha i valori più grande e più piccolo per nessuno

6. Intervalli di aumento e diminuzione: la funzione è crescente e decrescente di

7. Asintoti: X= 0 (asse UO) – asintoto verticale;

Y= 0 (asse OH) – asintoto orizzontale.

8. Grafici di funzioni Sono iperboli quadratiche (Fig. 5.5).

Funzione di potenza

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione non ha la proprietà dei pari e dei dispari.

4. Frequenza della funzione: non periodico.

5. Zeri di funzione: X= 0 – l'unico zero.

6. I valori più grandi e più piccoli della funzione: la funzione assume il valore più piccolo pari a 0 in quel punto X= 0; non ha più importanza.

7. Intervalli di aumento e diminuzione: la funzione è crescente nell'intero dominio di definizione.

8. Ciascuna di queste funzioni per un certo esponente è l'inverso della funzione fornita

9. Grafico di una funzione"assomiglia" al grafico di una funzione per qualsiasi N ed è mostrato in Fig. 5.6.

Funzione di potenza

1. Dominio:

2. Significati multipli:

3. Pari e dispari: la funzione è strana.

4. Frequenza della funzione: non periodico.

5. Zeri di funzione: X= 0 – l'unico zero.

6. I valori più grandi e più piccoli della funzione: la funzione non ha i valori più grande e più piccolo per nessuno

7. Intervalli di aumento e diminuzione: la funzione è crescente nell'intero dominio di definizione.

8. Grafico di una funzione Mostrato nella fig. 5.7.

Vengono presentate le proprietà e i grafici delle funzioni di potenza per vari valori dell'esponente. Formule di base, domini di definizione e insiemi di valori, parità, monotonicità, crescente e decrescente, estremi, convessità, flessioni, punti di intersezione con assi coordinati, limiti, valori particolari.

Formule con funzioni di potenza

Nel dominio di definizione della funzione potenza y = x p valgono le seguenti formule:
; ;
;
; ;
; ;
; .

Proprietà delle funzioni potenza e loro grafici

Funzione di potenza con esponente pari a zero, p = 0

Se l'esponente della funzione potenza y = x p è uguale a zero, p = 0, allora la funzione potenza è definita per tutti gli x ≠ 0 ed è una costante uguale a uno:
y = x p = x 0 = 1, x ≠ 0.

Funzione di potenza con esponente dispari naturale, p = n = 1, 3, 5, ...

Consideriamo una funzione di potenza y = x p = x n con esponente dispari naturale n = 1, 3, 5, ... . Questo indicatore può anche essere scritto nella forma: n = 2k + 1, dove k = 0, 1, 2, 3, ... è un numero intero non negativo. Di seguito sono riportate le proprietà e i grafici di tali funzioni.

Grafico di una funzione di potenza y = x n con esponente naturale dispari per vari valori dell'esponente n = 1, 3, 5, ... .

Dominio: -∞ < x < ∞
Significati multipli: -∞ < y < ∞
Parità: dispari, y(-x) = - y(x)
Monotono: aumenta monotonicamente
Estremi: NO
Convesso:
a -∞< x < 0 выпукла вверх
a 0< x < ∞ выпукла вниз
Punti di flesso: x = 0, y = 0
x = 0, y = 0
Limiti:
;
Valori privati:
in x = -1,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
in x = 0, y(0) = 0 n = 0
per x = 1, y(1) = 1 n = 1
Funzione inversa:
per n = 1, la funzione è il suo inverso: x = y
per n ≠ 1, la funzione inversa è la radice di grado n:

Funzione di potenza con esponente pari naturale, p = n = 2, 4, 6, ...

Consideriamo una funzione di potenza y = x p = x n con esponente pari naturale n = 2, 4, 6, ... . Questo indicatore può anche essere scritto nella forma: n = 2k, dove k = 1, 2, 3, ... - naturale. Le proprietà e i grafici di tali funzioni sono riportati di seguito.

Grafico di una funzione di potenza y = x n con esponente naturale pari per vari valori dell'esponente n = 2, 4, 6, ....

Dominio: -∞ < x < ∞
Significati multipli: 0 ≤ y< ∞
Parità: pari, y(-x) = y(x)
Monotono:
per x ≤ 0 diminuisce monotonicamente
per x ≥ 0 aumenta monotonicamente
Estremi: minimo, x = 0, y = 0
Convesso: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: x = 0, y = 0
Limiti:
;
Valori privati:
in x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
in x = 0, y(0) = 0 n = 0
per x = 1, y(1) = 1 n = 1
Funzione inversa:
per n = 2, radice quadrata:
per n ≠ 2, radice di grado n:

Funzione di potenza con esponente intero negativo, p = n = -1, -2, -3, ...

Considera una funzione di potenza y = x p = x n con un esponente intero negativo n = -1, -2, -3, ... . Se poniamo n = -k, dove k = 1, 2, 3, ... è un numero naturale, allora può essere rappresentato come:

Grafico di una funzione di potenza y = x n con esponente intero negativo per vari valori dell'esponente n = -1, -2, -3, ... .

Esponente dispari, n = -1, -3, -5, ...

Di seguito sono riportate le proprietà della funzione y = x n con esponente negativo dispari n = -1, -3, -5, ....

Dominio: x ≠ 0
Significati multipli: y ≠ 0
Parità: dispari, y(-x) = - y(x)
Monotono: diminuisce monotonicamente
Estremi: NO
Convesso:
all'x< 0 : выпукла вверх
per x > 0: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: NO
Cartello:
all'x< 0, y < 0
per x > 0, y > 0
Limiti:
; ; ;
Valori privati:
per x = 1, y(1) = 1 n = 1
Funzione inversa:
quando n = -1,
al n< -2 ,

Esponente pari, n = -2, -4, -6, ...

Di seguito sono riportate le proprietà della funzione y = x n con esponente pari negativo n = -2, -4, -6, ....

Dominio: x ≠ 0
Significati multipli: y > 0
Parità: pari, y(-x) = y(x)
Monotono:
all'x< 0 : монотонно возрастает
per x > 0: diminuisce monotonicamente
Estremi: NO
Convesso: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: NO
Cartello: y > 0
Limiti:
; ; ;
Valori privati:
per x = 1, y(1) = 1 n = 1
Funzione inversa:
a n = -2,
al n< -2 ,

Funzione di potenza con esponente razionale (frazionario).

Considera una funzione di potenza y = x p con un esponente razionale (frazionario), dove n è un numero intero, m > 1 è un numero naturale. Inoltre n, m non hanno divisori comuni.

Il denominatore dell'indicatore frazionario è dispari

Sia dispari il denominatore dell'esponente frazionario: m = 3, 5, 7, ... . In questo caso, la funzione potenza x p è definita sia per i valori positivi che negativi dell'argomento x. Consideriamo le proprietà di tali funzioni di potenza quando l'esponente p rientra entro certi limiti.

Il valore p è negativo, p< 0

Sia l'esponente razionale (con denominatore dispari m = 3, 5, 7, ...) minore di zero: .

Grafici di funzioni di potenza con esponente razionale negativo per vari valori dell'esponente, dove m = 3, 5, 7, ... è dispari.

Numeratore dispari, n = -1, -3, -5, ...

Presentiamo le proprietà della funzione di potenza y = x p con un esponente negativo razionale, dove n = -1, -3, -5, ... è un intero negativo dispari, m = 3, 5, 7 ... è un intero naturale dispari.

Dominio: x ≠ 0
Significati multipli: y ≠ 0
Parità: dispari, y(-x) = - y(x)
Monotono: diminuisce monotonicamente
Estremi: NO
Convesso:
all'x< 0 : выпукла вверх
per x > 0: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: NO
Cartello:
all'x< 0, y < 0
per x > 0, y > 0
Limiti:
; ; ;
Valori privati:
in x = -1, y(-1) = (-1) n = -1
per x = 1, y(1) = 1 n = 1
Funzione inversa:

Numeratore pari, n = -2, -4, -6, ...

Proprietà della funzione di potenza y = x p con esponente razionale negativo, dove n = -2, -4, -6, ... è un intero negativo pari, m = 3, 5, 7 ... è un intero naturale dispari .

Dominio: x ≠ 0
Significati multipli: y > 0
Parità: pari, y(-x) = y(x)
Monotono:
all'x< 0 : монотонно возрастает
per x > 0: diminuisce monotonicamente
Estremi: NO
Convesso: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: NO
Cartello: y > 0
Limiti:
; ; ;
Valori privati:
in x = -1, y(-1) = (-1) n = 1
per x = 1, y(1) = 1 n = 1
Funzione inversa:

Il valore p è positivo, inferiore a uno, 0< p < 1

Grafico di una funzione di potenza con esponente razionale (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.

Numeratore dispari, n = 1, 3, 5, ...

< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Dominio: -∞ < x < +∞
Significati multipli: -∞ < y < +∞
Parità: dispari, y(-x) = - y(x)
Monotono: aumenta monotonicamente
Estremi: NO
Convesso:
all'x< 0 : выпукла вниз
per x > 0: convesso verso l'alto
Punti di flesso: x = 0, y = 0
Punti di intersezione con assi coordinati: x = 0, y = 0
Cartello:
all'x< 0, y < 0
per x > 0, y > 0
Limiti:
;
Valori privati:
in x = -1, y(-1) = -1
in x = 0, y(0) = 0
per x = 1, y(1) = 1
Funzione inversa:

Numeratore pari, n = 2, 4, 6, ...

Vengono presentate le proprietà della funzione di potenza y = x p con esponente razionale compreso tra 0< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Dominio: -∞ < x < +∞
Significati multipli: 0 ≤ y< +∞
Parità: pari, y(-x) = y(x)
Monotono:
all'x< 0 : монотонно убывает
per x > 0: aumenta monotonicamente
Estremi: minimo in x = 0, y = 0
Convesso: convesso verso l'alto per x ≠ 0
Punti di flesso: NO
Punti di intersezione con assi coordinati: x = 0, y = 0
Cartello: per x ≠ 0, y > 0
Limiti:
;
Valori privati:
in x = -1, y(-1) = 1
in x = 0, y(0) = 0
per x = 1, y(1) = 1
Funzione inversa:

L'indice p è maggiore di uno, p > 1

Grafico di una funzione di potenza con esponente razionale (p > 1) per vari valori dell'esponente, dove m = 3, 5, 7, ... è dispari.

Numeratore dispari, n = 5, 7, 9, ...

Proprietà della funzione potenza y = x p con esponente razionale maggiore di uno: . Dove n = 5, 7, 9, ... - naturale dispari, m = 3, 5, 7 ... - naturale dispari.

Dominio: -∞ < x < ∞
Significati multipli: -∞ < y < ∞
Parità: dispari, y(-x) = - y(x)
Monotono: aumenta monotonicamente
Estremi: NO
Convesso:
a -∞< x < 0 выпукла вверх
a 0< x < ∞ выпукла вниз
Punti di flesso: x = 0, y = 0
Punti di intersezione con assi coordinati: x = 0, y = 0
Limiti:
;
Valori privati:
in x = -1, y(-1) = -1
in x = 0, y(0) = 0
per x = 1, y(1) = 1
Funzione inversa:

Numeratore pari, n = 4, 6, 8, ...

Proprietà della funzione potenza y = x p con esponente razionale maggiore di uno: . Dove n = 4, 6, 8, ... - naturale pari, m = 3, 5, 7 ... - naturale dispari.

Dominio: -∞ < x < ∞
Significati multipli: 0 ≤ y< ∞
Parità: pari, y(-x) = y(x)
Monotono:
all'x< 0 монотонно убывает
per x > 0 aumenta monotonicamente
Estremi: minimo in x = 0, y = 0
Convesso: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: x = 0, y = 0
Limiti:
;
Valori privati:
in x = -1, y(-1) = 1
in x = 0, y(0) = 0
per x = 1, y(1) = 1
Funzione inversa:

Il denominatore dell'indicatore frazionario è pari

Sia pari il denominatore dell'esponente frazionario: m = 2, 4, 6, ... . In questo caso la funzione potenza x p non è definita per valori negativi dell'argomento. Le sue proprietà coincidono con le proprietà di una funzione di potenza con esponente irrazionale (vedi la sezione successiva).

Funzione di potenza con esponente irrazionale

Consideriamo una funzione di potenza y = x p con esponente irrazionale p. Le proprietà di tali funzioni differiscono da quelle discusse sopra in quanto non sono definite per valori negativi dell'argomento x. Per valori positivi dell'argomento, le proprietà dipendono solo dal valore dell'esponente p e non dipendono dal fatto che p sia intero, razionale o irrazionale.

y = x p per diversi valori dell'esponente p.

Funzione potenza con esponente negativo p< 0

Dominio: x > 0
Significati multipli: y > 0
Monotono: diminuisce monotonicamente
Convesso: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: NO
Limiti: ;
Significato privato: Per x = 1, y(1) = 1 p = 1

Funzione di potenza con esponente positivo p > 0

Indicatore inferiore a uno 0< p < 1

Dominio: x≥ 0
Significati multipli: y ≥ 0
Monotono: aumenta monotonicamente
Convesso: convesso verso l'alto
Punti di flesso: NO
Punti di intersezione con assi coordinati: x = 0, y = 0
Limiti:
Valori privati: Per x = 0, y(0) = 0 p = 0 .
Per x = 1, y(1) = 1 p = 1

L’indicatore è maggiore di un p > 1

Dominio: x≥ 0
Significati multipli: y ≥ 0
Monotono: aumenta monotonicamente
Convesso: convesso verso il basso
Punti di flesso: NO
Punti di intersezione con assi coordinati: x = 0, y = 0
Limiti:
Valori privati: Per x = 0, y(0) = 0 p = 0 .
Per x = 1, y(1) = 1 p = 1

Riferimenti:
IN. Bronstein, K.A. Semendyaev, Manuale di matematica per ingegneri e studenti universitari, “Lan”, 2009.

Per comodità di considerare una funzione di potenza, considereremo 4 casi separati: una funzione di potenza con esponente naturale, una funzione di potenza con esponente intero, una funzione di potenza con esponente razionale e una funzione di potenza con esponente irrazionale.

Funzione potenza con esponente naturale

Per prima cosa introduciamo il concetto di laurea con esponente naturale.

Definizione 1

La potenza di un numero reale $a$ con esponente naturale $n$ è un numero uguale al prodotto di $n$ fattori, ciascuno dei quali è uguale al numero $a$.

Immagine 1.

$a$ è la base della laurea.

$n$ è l'esponente.

Consideriamo ora una funzione di potenza con esponente naturale, le sue proprietà e il suo grafico.

Definizione 2

$f\left(x\right)=x^n$ ($n\in N)$ è detta funzione di potenza con esponente naturale.

Per maggiore comodità, consideriamo separatamente una funzione di potenza con esponente pari $f\left(x\right)=x^(2n)$ e una funzione di potenza con esponente dispari $f\left(x\right)=x^ (2n-1)$ ($n\in N)$.

Proprietà di una funzione di potenza con esponente naturale pari

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ -- la funzione è pari.

Area del valore -- $\

La funzione diminuisce come $x\in (-\infty ,0)$ e aumenta come $x\in (0,+\infty)$.

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1 ))\ge 0$

La funzione è convessa su tutto il dominio di definizione.

Comportamento alle estremità del dominio:

\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]

Grafico (Fig. 2).

Figura 2. Grafico della funzione $f\left(x\right)=x^(2n)$

Proprietà di una funzione di potenza con esponente naturale dispari

Il dominio di definizione sono tutti i numeri reali.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- la funzione è dispari.

$f(x)$ è continua nell'intero dominio di definizione.

L'intervallo è composto da tutti numeri reali.

$f"\sinistra(x\destra)=\sinistra(x^(2n-1)\destra)"=(2n-1)\cdot x^(2(n-1))\ge 0$

La funzione aumenta lungo l'intero dominio di definizione.

$f\sinistra(x\destra)0$, per $x\in (0,+\infty)$.

$f(""\sinistra(x\destra))=(\sinistra(\sinistra(2n-1\destra)\cdot x^(2\sinistra(n-1\destra))\destra))"=2 \sinistra(2n-1\destra)(n-1)\cdot x^(2n-3)$

\ \

La funzione è concava per $x\in (-\infty ,0)$ e convessa per $x\in (0,+\infty)$.

Grafico (Fig. 3).

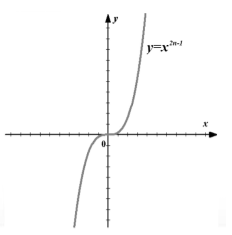
Figura 3. Grafico della funzione $f\left(x\right)=x^(2n-1)$

Funzione di potenza con esponente intero

Innanzitutto, introduciamo il concetto di grado con esponente intero.

Definizione 3

La potenza di un numero reale $a$ con esponente intero $n$ è determinata dalla formula:

Figura 4.

Consideriamo ora una funzione di potenza con esponente intero, le sue proprietà e il suo grafico.

Definizione 4

$f\left(x\right)=x^n$ ($n\in Z)$ è chiamata funzione di potenza con esponente intero.

Se il grado è maggiore di zero si arriva al caso di una funzione potenza con esponente naturale. Ne abbiamo già parlato sopra. Per $n=0$ otteniamo una funzione lineare $y=1$. Lasceremo la sua considerazione al lettore. Resta da considerare le proprietà di una funzione di potenza con esponente intero negativo

Proprietà di una funzione di potenza con esponente intero negativo

Il dominio di definizione è $\left(-\infty ,0\right)(0,+\infty)$.

Se l'esponente è pari la funzione è pari; se è dispari la funzione è dispari.

$f(x)$ è continua nell'intero dominio di definizione.

Scopo:

Se l'esponente è pari, allora $(0,+\infty)$; se è dispari, allora $\left(-\infty ,0\right)(0,+\infty)$.

Per un esponente dispari, la funzione diminuisce come $x\in \left(-\infty ,0\right)(0,+\infty)$. Se l'esponente è pari, la funzione diminuisce come $x\in (0,+\infty)$. e aumenta come $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ sull'intero dominio di definizione

Funzione potenza con esponente naturale

Per prima cosa introduciamo il concetto di laurea con esponente naturale.

Definizione 1

La potenza di un numero reale $a$ con esponente naturale $n$ è un numero uguale al prodotto di $n$ fattori, ciascuno dei quali è uguale al numero $a$.

Immagine 1.

$a$ è la base della laurea.

$n$ è l'esponente.

Consideriamo ora una funzione di potenza con esponente naturale, le sue proprietà e il suo grafico.

Definizione 2

$f\left(x\right)=x^n$ ($n\in N)$ è detta funzione di potenza con esponente naturale.

Proprietà di una funzione di potenza con esponente naturale pari

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ -- la funzione è pari.

Area del valore -- $\

La funzione diminuisce come $x\in (-\infty ,0)$ e aumenta come $x\in (0,+\infty)$.

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1 ))\ge 0$

La funzione è convessa su tutto il dominio di definizione.

Comportamento alle estremità del dominio:

\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]

Grafico (Fig. 2).

Figura 2. Grafico della funzione $f\left(x\right)=x^(2n)$

Proprietà di una funzione di potenza con esponente naturale dispari

Il dominio di definizione sono tutti i numeri reali.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- la funzione è dispari.

$f(x)$ è continua nell'intero dominio di definizione.

L'intervallo è composto da tutti numeri reali.

$f"\sinistra(x\destra)=\sinistra(x^(2n-1)\destra)"=(2n-1)\cdot x^(2(n-1))\ge 0$

La funzione aumenta lungo l'intero dominio di definizione.

$f\sinistra(x\destra)0$, per $x\in (0,+\infty)$.

$f(""\sinistra(x\destra))=(\sinistra(\sinistra(2n-1\destra)\cdot x^(2\sinistra(n-1\destra))\destra))"=2 \sinistra(2n-1\destra)(n-1)\cdot x^(2n-3)$

\ \

La funzione è concava per $x\in (-\infty ,0)$ e convessa per $x\in (0,+\infty)$.

Grafico (Fig. 3).

Figura 3. Grafico della funzione $f\left(x\right)=x^(2n-1)$

Funzione di potenza con esponente intero

Innanzitutto, introduciamo il concetto di grado con esponente intero.

Definizione 3

La potenza di un numero reale $a$ con esponente intero $n$ è determinata dalla formula:

Figura 4.

Consideriamo ora una funzione di potenza con esponente intero, le sue proprietà e il suo grafico.

Definizione 4

$f\left(x\right)=x^n$ ($n\in Z)$ è chiamata funzione di potenza con esponente intero.

Proprietà di una funzione di potenza con esponente intero negativo

Il dominio di definizione è $\left(-\infty ,0\right)(0,+\infty)$.

Se l'esponente è pari la funzione è pari; se è dispari la funzione è dispari.

$f(x)$ è continua nell'intero dominio di definizione.

Scopo:

Se l'esponente è pari, allora $(0,+\infty)$; se è dispari, allora $\left(-\infty ,0\right)(0,+\infty)$.

$f(x)\ge 0$ sull'intero dominio di definizione